- 81までの九九表外の素数ではない奇数は全部で 9個あって、51と57に気をつければ、あとは素数ではないとすぐ見分けがつく数ばかりだということがわかりました。
- [33, 39, 51, 55, 57, 65, 69, 75, 77]
- ちなみに、81までの素数は、{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79}の22個で、はじめの4つ以外の18個はすべて九九表外です。
1. 問題
1から順番に素数を挙げていたら、間違えて「57」を言ってしまいました。
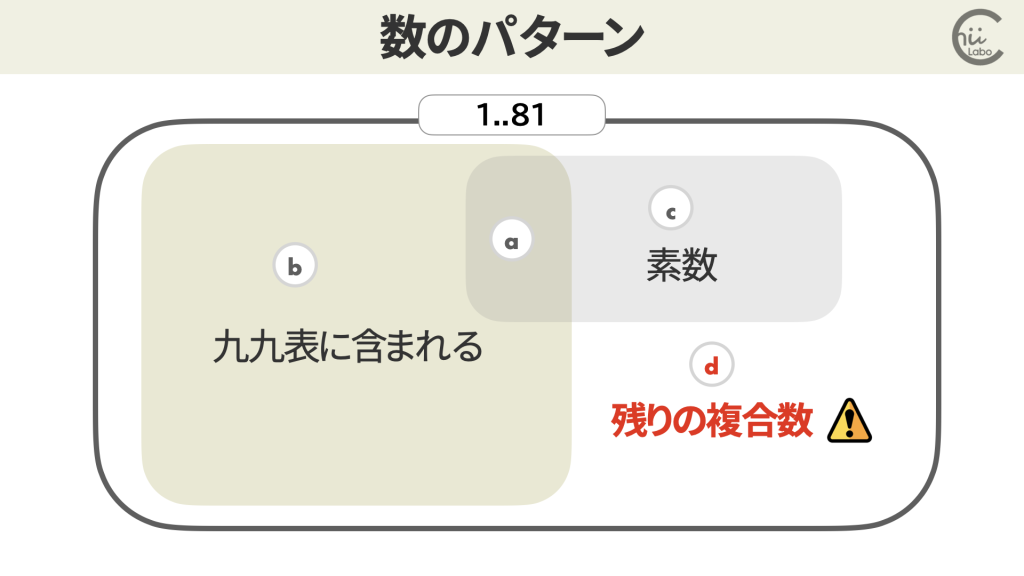
このように 81までの九九表に含まれない奇数でも、素数ではない数が紛れています。
このような数は、全部でいくつあるでしょうか?

ちなみに、1は素数じゃないよ。
2. 連番の集合(range)
Pythonで解いてみます。
まずは、考える全体の集合を作ってみます。
n = set(range(1, 82))
print(n)
print(len(n))この出力は、こうなります。
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81}
813. 条件で生成する集合(for, in)
九九表(times tables)の集合 t は、
t = set(i * j for i in range(1, 10) for j in range(1, 10))
print(t)
print(len(t))
出力は、
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 24, 25, 27, 28, 30, 32, 35, 36, 40, 42, 45, 48, 49, 54, 56, 63, 64, 72, 81}
36
81個マスはあるのに、意外と出てくる数のパターンは少ないんだね。
4. 差集合
九九表の外の数は、差集合で求められます。
print(n-t)
print(len(n-t)){11, 13, 17, 19, 22, 23, 26, 29, 31, 33, 34, 37, 38, 39, 41, 43, 44, 46, 47, 50, 51, 52, 53, 55, 57, 58, 59, 60, 61, 62, 65, 66, 67, 68, 69, 70, 71, 73, 74, 75, 76, 77, 78, 79, 80}
45
5. 条件による集合(filter)
ここで、素数の集合も作ってみます。
def is_prime(n):
if n < 2:
return False
for i in range(2, int(n**0.5) + 1):
if n % i == 0:
return False
return True
p = set(filter(is_prime, range(1, 82)))判定用の関数を作って、filterで絞り込みます。
{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79}
22
81までの素数は、22個なんだね。
九九表にない複合数も差集合で求められます。
print(n-t-p)
print(len(n-t-p)){22, 26, 33, 34, 38, 39, 44, 46, 50, 51, 52, 55, 57, 58, 60, 62, 65, 66, 68, 69, 70, 74, 75, 76, 77, 78, 80}
27
意外と多いね。
でも、よく見ると偶数も多い。
これは、すぐに素数ではないとわかるね。
6. 等差数列の集合(range)・積集合
まずは、奇数の集合を作って、積集合を作ると、
o = set(range(1, 82, 2))
print(o & (n-t-p))
print(len(o & (n-t-p)))
結果は、
{33, 65, 69, 39, 75, 77, 51, 55, 57}
9これを昇順に並べると、
sorted(o & (n-t-p))
#=>[33, 39, 51, 55, 57, 65, 69, 75, 77]
だいぶ減ったね。
だけど、5の倍数と、11の倍数は、見るからに複合数。
素数とは間違えなさそう。
7. 条件式による集合(in, if)
x = o & (n-t-p))
y = {n for n in x if n % 5 != 0 and n % 11 != 0}
{39, 51, 57, 69}
うーん、39や69も3の倍数だと、すぐわかる。
結果、一番 素数と間違えそうなのは、51と57なんだけど……
まぁ、3の倍数なんだね。
8. 結果の表
| 九九表内 | 九九表外 | |
|---|---|---|
| 素数 | 4 | 18 |
| 複合数 | 32 | 奇数:9 偶数:18 |
結果、九九表外の素数ではない奇数は全部で 9個あって、51と57に気をつければ、あとは素数ではないとすぐ見分けがつく数ばかりだということがわかりました。
n = {i for i in range(1,81)}
t = set(i * j for i in range(1, 10) for j in range(1, 10))
def is_prime(n):
if n < 2:
return False
for i in range(2, int(n**0.5) + 1):
if n % i == 0:
return False
return True
p = set(filter(is_prime, range(1, 82)))
o = set(range(1, 82, 2))
x = o & (n-t-p)
y = {n for n in x if n % 5 != 0 and n % 11 != 0}
print(y) #=> {39, 51, 57, 69}
こちらもどうぞ。



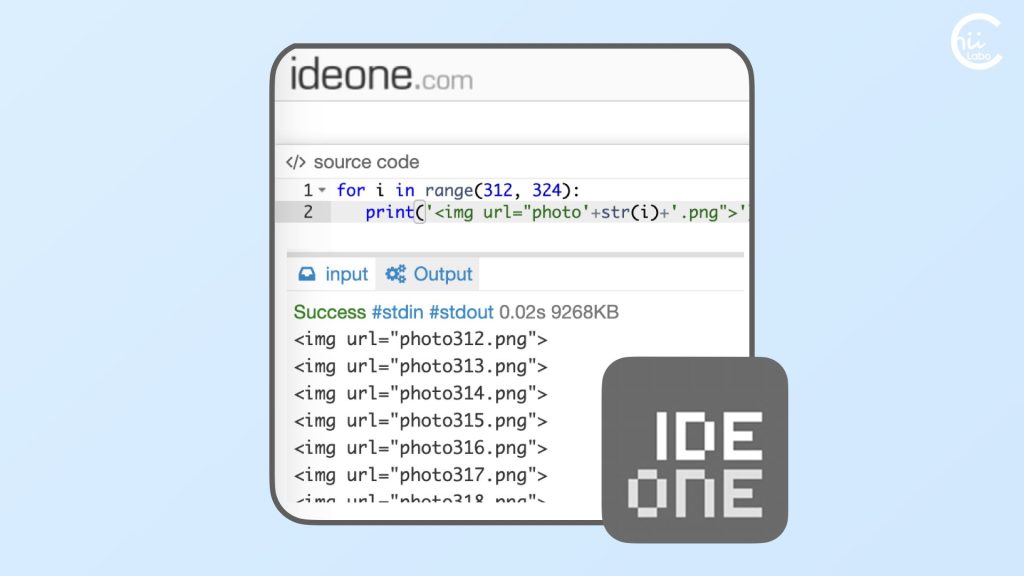
手軽にプログラミングするならオンラインIDEが便利(ideone.com)
たまに、連番の文字列を入力したいなど、ちょっとした単純作業をプログラムで処理したい場合があります。しかし、その時のパソコンによってプログラミング環境があったり、なかったり。久しぶりに使うと、そのタイミングでアップデートから用意しないといけません。そんなときにすぐに使えるのが、オンラインIDE(統合開発環境)。インターネット上にコードを入力するだけで、かんたんな出力結果を得ることができます。(サイト)for i in range(312, 324): print('<img u...
当たり前だけどプログラミング言語の教科書は進歩している(『スッキリわかるC言語入門』のアプローチ)
インターネットを見ていたら、たまたま「堅苦しいCの教科書に疲れたらー」という広告が目に止まりました。刺さるキャッチコピーだと思いました。今回は、『スッキリわかるC言語入門』のアプローチをもとに、プログラミング言語の進歩について考えてみます。ポイントC言語も使いやすくなっている。開発環境の準備も手軽になっている。常識は変わるもの。書籍のPR記事ではありませんが、興味があれば手にとって見てください。「堅苦しい教科書」ではないこちらが広告の大きいサイズです。本もネット広告を出すんだ...

どこからはじめる?子どものプログラミング教育【プログラミング的思考】
最近、話題の「プログラミング教育」。今日は、子どものプログラミングを学ぶ意味や学習法について、基本の話から一緒に考えてみましょう。学習指導要領によると…プログラミングは魔法のことばまずは実際にプログラムをみてみましょう。/* v2.0 | 20110126 License: none (public domain)*//*Above is my default quick CSS reset I always use, doesn't really matter for th...
QRコードを読み込むと、関連記事を確認できます。




![[Cocoon] 「SNSシェア」ボタンをショートコードで表示できるようにした](https://chiilabo.com/wp-content/uploads/2024/02/image-37-1-1024x576.jpg)