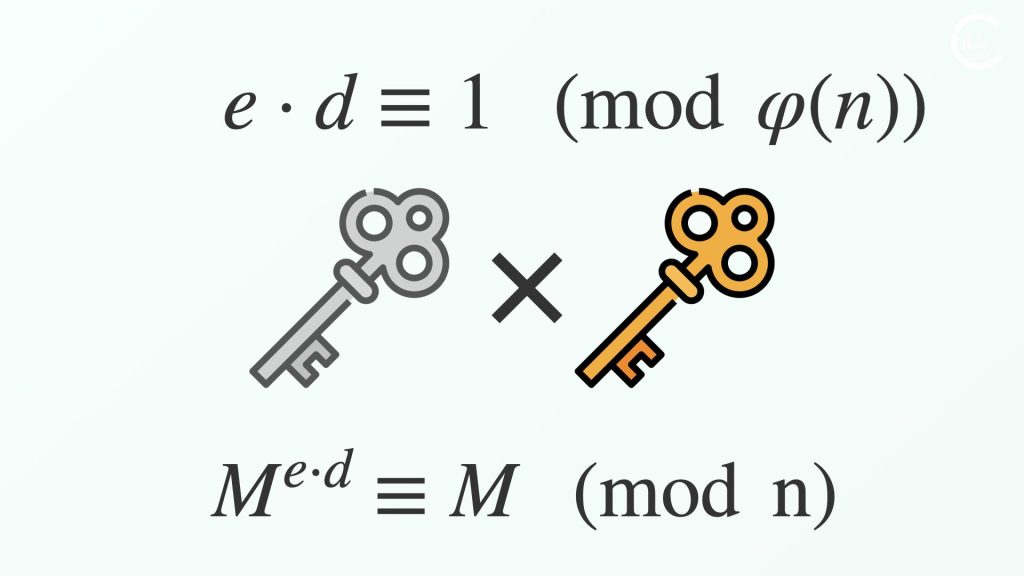- 「RSA暗号」は、数学的な性質を利用して秘密通信を可能にする暗号システムです。
- 公開鍵と秘密鍵の組み合わせで、メッセージの暗号化と復号ができます。
1. 元に戻せてこそ「暗号」
暗号で大事なことは「わけのわからんデータにし、後で元に戻せる」ということです。
「RSA暗号」では、累乗していくと nで割った余りが周期的に元に戻る、という数の性質を利用しています。
ざっくり説明すると、重ね合わせると一周回るように2つの鍵を作っています。
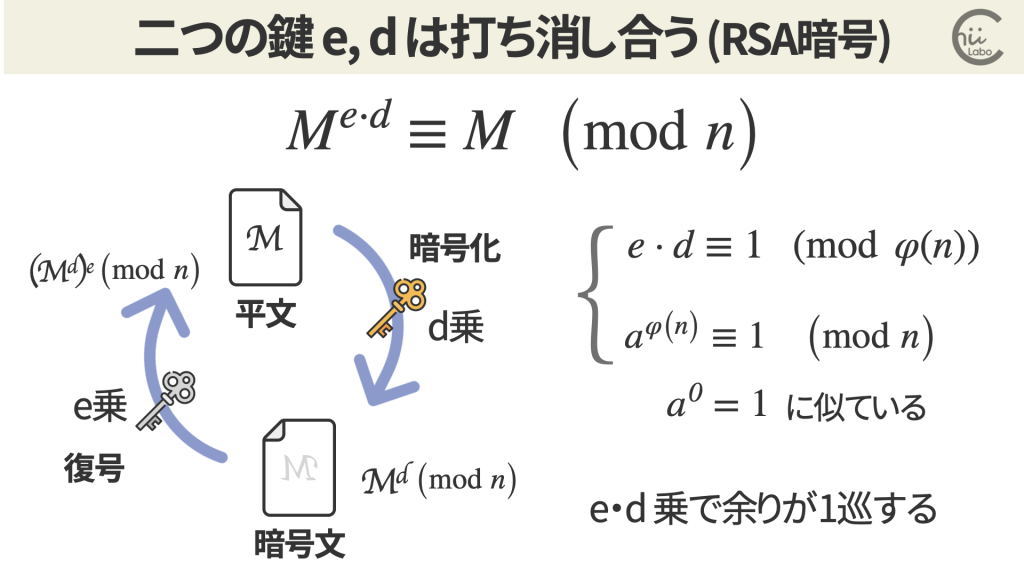
この性質は、「オイラーの定理」が根底にあります。

急に出てきたφ(n)を使う意味など、おいおい説明していきます。
2. 秘密鍵と公開鍵の作り方

秘密鍵と公開鍵の具体的な例として、RSA暗号システムの小さな数値を使用してみます。
アリスさんとボブさんは出会ったときに、後でボブさんがアリスさんのメッセージを確認できるように考えました。
そこで、アリスさんは公開鍵と秘密鍵を作ることにしました。
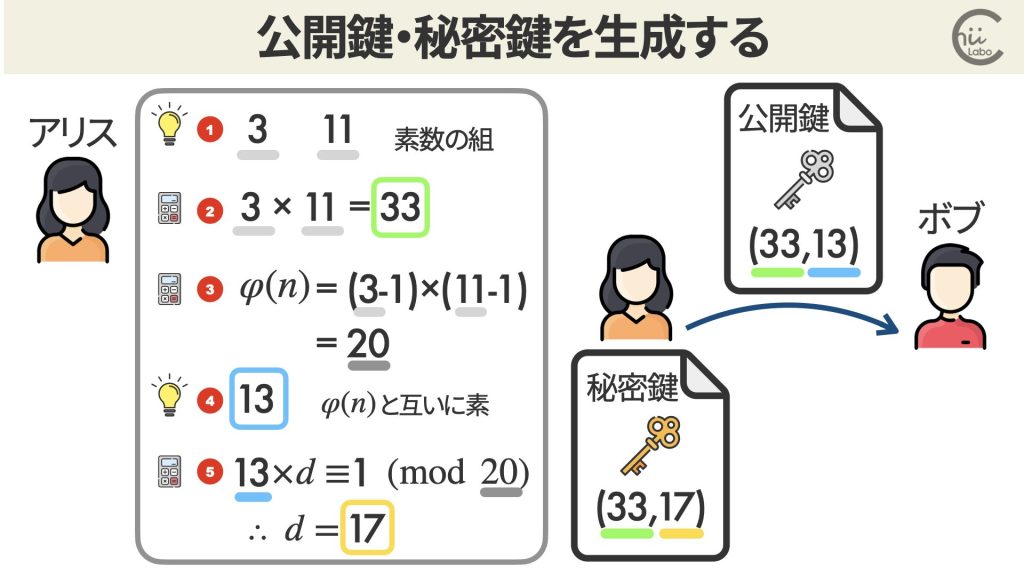

まだ意味がわからなくても「レシピ」に従えば、誰でも作れます。
2.1. 気合いで秘密鍵を探してみる

秘密鍵 d は、どうやって計算したの?
とりあえず、ここでは「しらみつぶし」で探してみます。
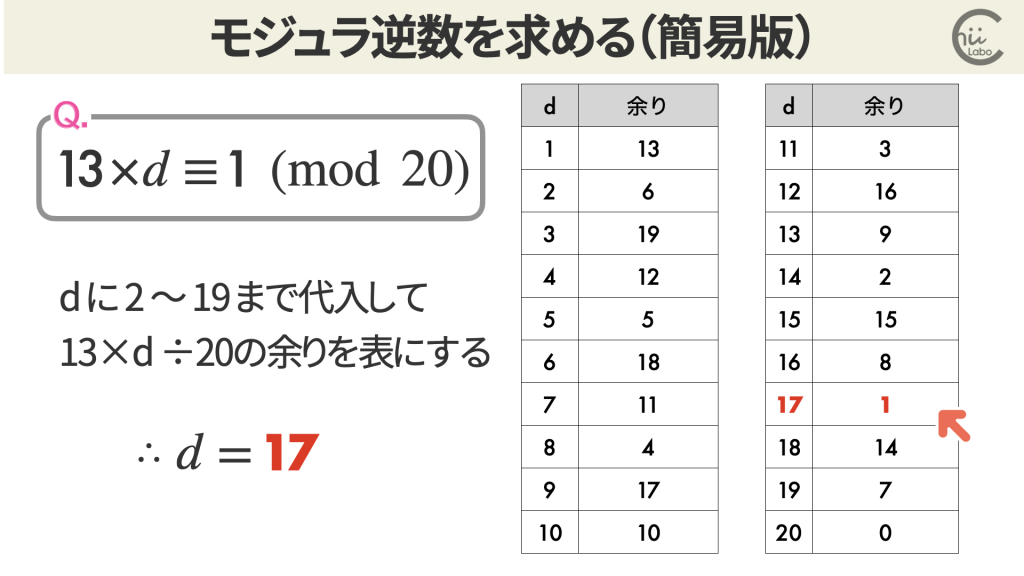

より効率的な求め方は、後ほど説明します。
print("| d | 13*d mod 20 |")
print("|---|-------------|")
for d in range(2, 20):
result = (13 * d) % 20
print(f"| {d:2d} | {result:11d} |")ちなみに、e × d をφ(n)で割った余りが1となるので、
dは「法φ(n)での eのモジュラ逆数」と言えます。
2.2. 公開鍵の情報を渡す
計算された n, e, d から公開鍵と秘密鍵を作ります。
- 公開鍵: (n, e) = (33, 13)
- 秘密鍵: (n, d) = (33, 17)
ボブさんには公開鍵を渡し、
秘密鍵はアリスさんだけが持ちます。
3. チャレンジのリクエスト

さっきの複雑な計算は何のため?
それは、この3つの数 n, e, d には特別な性質があるからです。
後日、ボブさんは、アリスさんっぽい人に出会いました。
ボブさんは相手が本当にアリスさんなのか、ちゃんと秘密鍵を持っているか確認したいと考えました。
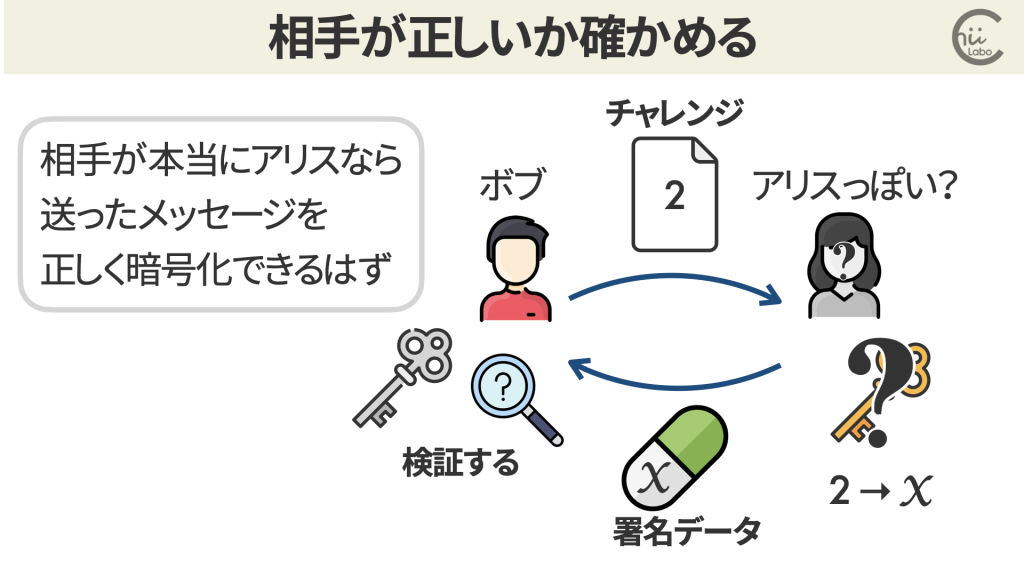
そこで、あるメッセージを暗号化して送り返すように依頼しました(チャレンジのリクエスト)。
たとえば、これをメッセージ M = 2 とします。
3.1. メッセージから署名を作る
実は相手の人は、本当にアリスさんでした。
アリスさんは、送られたメッセージに対応した暗号化データ(署名)を計算します。
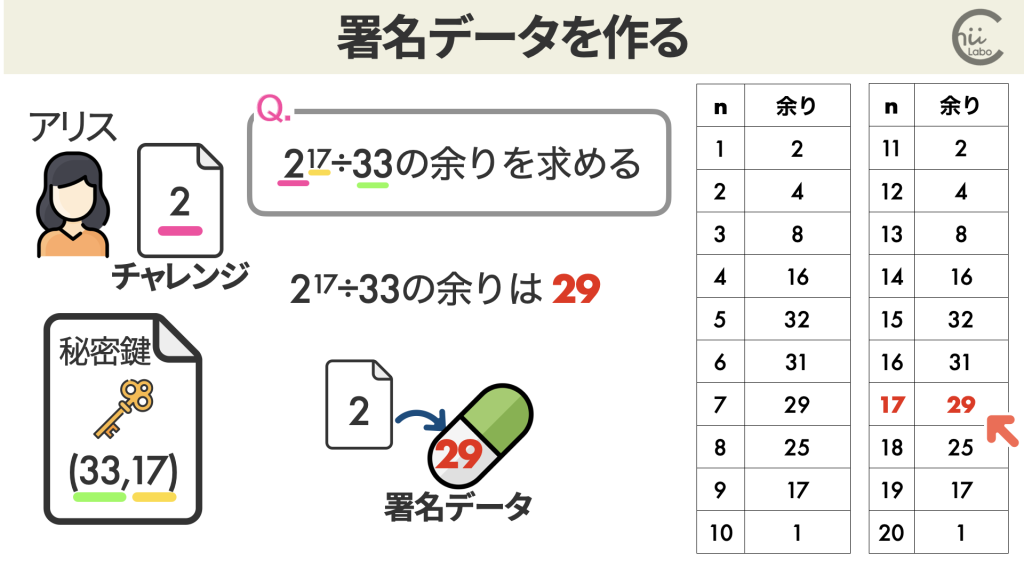
メッセージを秘密指数 dで累乗し n で余りを計算して、署名データ(s)にします。
今回は秘密鍵が(33, 17)なので、
s ≡ 2^17 ≡ 29 (mod 33)
アリスさんは、署名データ 29 を送り返しました。
3.2. 送られた署名を検証する
ボブさんは、受け取った署名データ 29 を復号します。

今度は署名データを公開指数で累乗し n で割った余りを確認します
アリスさんからもらった公開鍵 (33, 13) を使うと、
29^13 ≡ 2 (mod 33)
はじめに送ったメッセージと同じになりました。
なので、「メッセージ相手が秘密鍵を持っている」ということがわかりました。

つまり、アリスさんだと確認できたんだね。
3.3. 【補足】公開鍵でも暗号化できる
今回は、秘密鍵で暗号化し公開鍵で復号しましたが、逆の順でも同じです。
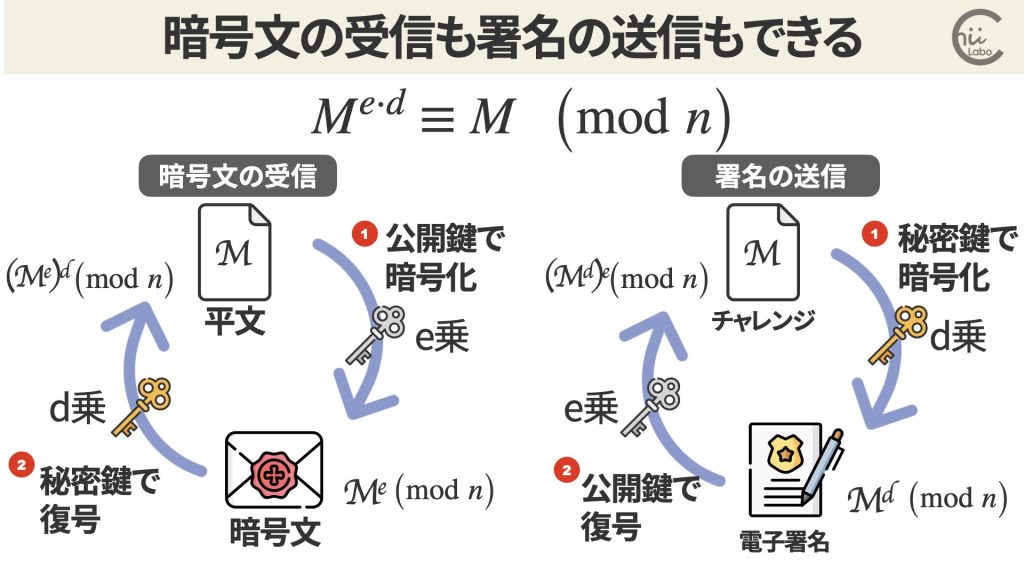
アリスさんにしか開けられない暗号文を受信したい場合には、相手に渡した公開鍵で暗号化してもらいます。

どっちかの鍵が暗号化専用とかではないんだね。
4. もし、他人ならどうなる?
もし、ボブさんが出会った相手がアリスさんではなかった場合はどうなるのでしょう?
たとえば、マロリーさんは秘密鍵がないので、メッセージ m = 2 に対して何を返したらよいかわかりません。
そこで、マロリーさんは適当に 8 をボブさんに返したとします。
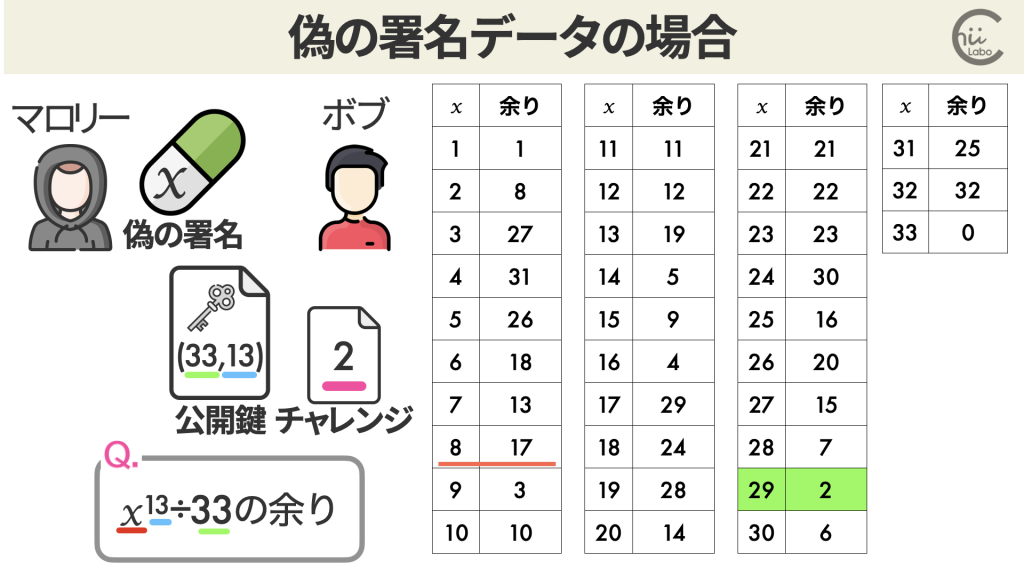
ボブさんは、いつも通り公開鍵を元に復号します。
m’ ≡ 8 ^13 ≡ 17 (mod 33)
29 以外の数字だと、元の数字 2 には戻りません。
これで、「メッセージの相手は秘密鍵を持っていない」ことがわかりました。
4.1. もっと複雑な秘密鍵・公開鍵を使う
ただし、この方法では偶然 同じ署名を送ってくることも考えられます。
そこで、実際のシステムでは、もっと大きな素数の組が使われるのが一般的です。
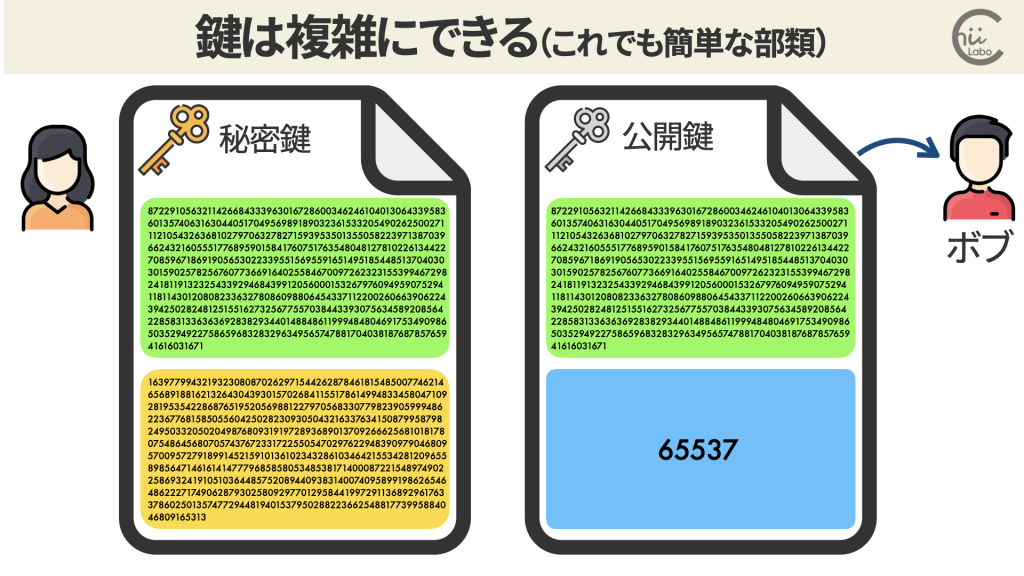
たとえば、1024ビットの素数(10進数の約309桁に相当)から生成するなら、
- n は約2048ビット(約617桁)の数になります。
- e は一般的に 65537(2^16 + 1)を使用し、
- d も非常に大きな数(約2048ビット:約617桁)になります。

まるで暗号みたいな数字列だけど、ちゃんと数値なんだね。

今回は、数値であることがわかりやすいように10進数で表記しました。
通常はA〜Fまで含む16進数で表記します。
たとえば、二つの素数(p, q)をこのように選ぶとします。
p = 132918245823130563424215976439036711668266663251266976750801495254719369947924460128149200687400543675905598300329808352854182145672616969700455009016977255032853036373338217354467094919269138985713548446263655094310853878552679065648761957819766588731584563808895086860244793939345553057091184917061285089279
q = 65626133637203457871338796511507795690060122668232404827999323889199363976064478936876553394856597812683270225689706863984149694946694115830007067153106366156668550453586755591046183215093059525625913185528751605624155589176255700955446562786335684905864598470434629799122105205040983376383577451739443583049公開鍵(n, e)を10進数表記するなら、このようになります。
公開鍵 (n, e):
n = 8722910563211426684333963016728600346246104013064339583601357406316304405170495698918903236153320549026250027111210543263681027970632782715939535013550582239713870396624321605551776895901584176075176354804812781022613442270859671869190565302233955156955916514951854485137040303015902578256760773669164025584670097262323155399467298241811913232543392946843991205600015326797609495907529411811430120808233632780860988064543371122002606639062243942502824812515516273256775570384433930756345892085642285831336363692838293440148848611999484804691753490986503529492275865968328329634956574788170403818768785765941616031671
e = 65537秘密鍵 dは、
秘密鍵 (n, d):
n = 8722910563211426684333963016728600346246104013064339583601357406316304405170495698918903236153320549026250027111210543263681027970632782715939535013550582239713870396624321605551776895901584176075176354804812781022613442270859671869190565302233955156955916514951854485137040303015902578256760773669164025584670097262323155399467298241811913232543392946843991205600015326797609495907529411811430120808233632780860988064543371122002606639062243942502824812515516273256775570384433930756345892085642285831336363692838293440148848611999484804691753490986503529492275865968328329634956574788170403818768785765941616031671
d = 1639779943219323080870262971544262878461815485007746214656891881621326430439301570268411551786149948334580471092819535422868765195205698812279705683307798239059994862236776815850556042502823093050432163376341508799587982495033205020498768093191972893689013709266625681018178075486456807057437672331722550547029762294839097904680957009572791899145215910136102343286103464215534281209655898564714616141477796858580534853817140008722154897490225869324191051036448575208944093831400740958991986265464862227174906287930258092977012958441997291136892961763378602501357477294481940153795028822366254881773995884046809165313この秘密鍵 d で メッセージ m = 12345 を暗号化します。
m^d mod n を計算するのは大変ですが、
Pythonには、効率的に処理する関数 pow があるので、かんたんに求められます2。
pow(base, exponent, modulus)暗号化されたメッセージ: 7202915292647932543509879307422138072309829989924522268153992133340396137077688367968526131073752914959449591647090358845924577216510648116390265269806233021042415093939673922394574600866643658750618843748813858814054582208035458487969082088543076901143422404760089467220841186493320898441794852100225299648331559964499221477430940579406090099409519127022236601068784698525914672732741300910791773583736587914489069185683823728609402973629790612660038573870171593059596159668447455108231626673363155295638802038487550438575490505483782367996772500536447978042553465050654019876142142860218888235636596444753105045757このメッセージは、公開鍵 eで復号化すると 12345 に戻ります。
import random
def is_prime(n, k=5):
if n < 2: return False
for p in [2,3,5,7,11,13,17,19,23,29]:
if n % p == 0: return n == p
s, d = 0, n-1
while d % 2 == 0:
s, d = s+1, d//2
for _ in range(k):
x = pow(random.randint(2, n-1), d, n)
if x == 1 or x == n-1: continue
for _ in range(s-1):
x = pow(x, 2, n)
if x == n-1: break
else: return False
return True
def generate_large_prime(bits):
while True:
n = random.getrandbits(bits)
if is_prime(n):
return n
def mod_inverse(a, m):
def egcd(a, b):
if a == 0: return (b, 0, 1)
g, y, x = egcd(b%a, a)
return (g, x - (b//a) * y, y)
g, x, _ = egcd(a, m)
if g != 1: raise Exception('Modular inverse does not exist')
return x % m
# キーの生成
bits = 1024
p = generate_large_prime(bits)
q = generate_large_prime(bits)
n = p * q
phi = (p - 1) * (q - 1)
e = 65537 # 一般的に使用される公開指数
d = mod_inverse(e, phi)
print(f"素数 (p, q):\np = {p}\n\nq = {q}\n")
print(f"公開鍵 (n, e):\nn = {n}\n\ne = {e}\n")
print(f"秘密鍵 (n, d):\nn = {n}\n\nd = {d}\n")
# メッセージの暗号化と復号化
message = 12345
encrypted = pow(message, d, n)
decrypted = pow(encrypted, e, n)
print(f"元のメッセージ: {message}")
print(f"暗号化されたメッセージ: {encrypted}")
print(f"復号化されたメッセージ: {decrypted}")
4.2. 選ぶ素数が小さいと秘密鍵が「バレる」
また、はじめに選んだ素数が小さいと秘密鍵を「当てる」こともできてしまいます。
まず、公開鍵の 33 から素数のペアを調べるには、小さい順に素数で割っていって割り切れるものを探します。
素数のペアがわかってしまえば、公開鍵から秘密鍵を求めることができます。
5. 【考察】暗号化と復号ができる理由
この暗号化・復号は、累乗の剰余の周期性を利用しています。

どうして33で割った余りは20乗で1周するの?
一般に aとnが互いに素であるとき、
aのべき乗をnで割った余りは、ある周期で繰り返されます。
ここでは、厳密な証明ではなくイメージで理解してみます。
aの1乗、2乗、3乗…と nで割った余りのパターンを考えていきます。
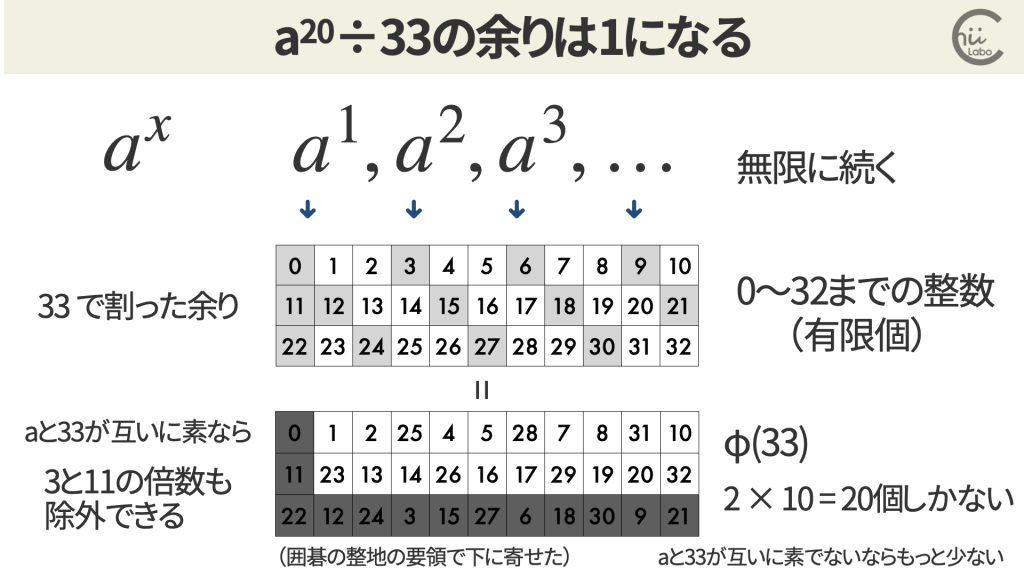
すると、いつかは同じ余りが出てくるはずです。
これは、nで割った余りは0からn-1までの n個しかないからです。
また、余りのパターンはさらに n個より絞れます。
aとnが互いに素なら、その積も n と互いに素になります。
そのため、aの1乗、2乗、3乗 … をnで割った余りも、常にnと互いに素になります。
つまり、nより小さくてnと互いに素な数の個数に限られるのです。
オイラーは、この「nより小さくてnと互いに素な数の個数」を、トーシェント関数φ(n)と定義しました。
つまり、周期の長さは最大でもφ(n)と言えます(もっと小さいφ(n)の約数のこともあります)。
今回は、nが素数(p, q)の積で表させるので、φ(n)は 1〜 n の中から pの倍数、qの倍数を除くことになります。
これは (p-1)×(q-1)で計算できます。
φ(n)個目の余りは、必ず一周して元に戻ってくるはずです。
これを数式で書いたのがオイラーの定理でした。
この定理は、nで割った余りの世界で指数関数で、
φ(n)が「0(単位元)」のような役割を果たすことを示しています。
そして同じ余りが出たら、そこからまた同じパターンが繰り返されます。
5.1. 2つの鍵で累乗すると余りは元に戻る
この性質を使って暗号化と復号を説明します。
e d ≡ 1 (mod φ(n)) を元にすると、
整数 kを使って
e d = 1 + k * φ(n) と表せます。
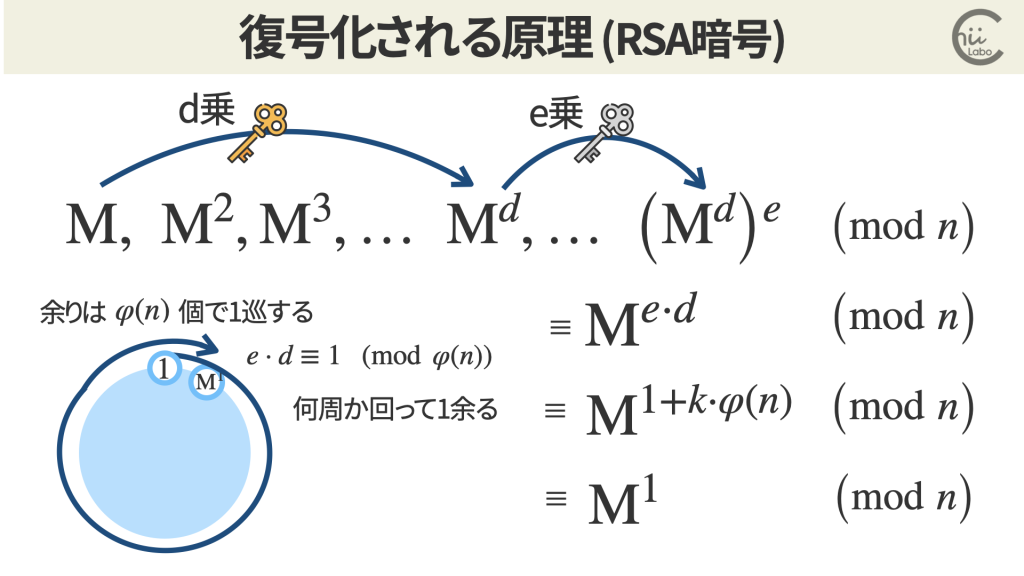
これは、余りのパターンでいうと何周か回って 1 余ることを表しています。
つまり、
と表すことができます。
この式の n で割った余りをみて、
オイラーの定理から(ただし、Mとnが互いに素の場合)、
これを代入すると、
となります。
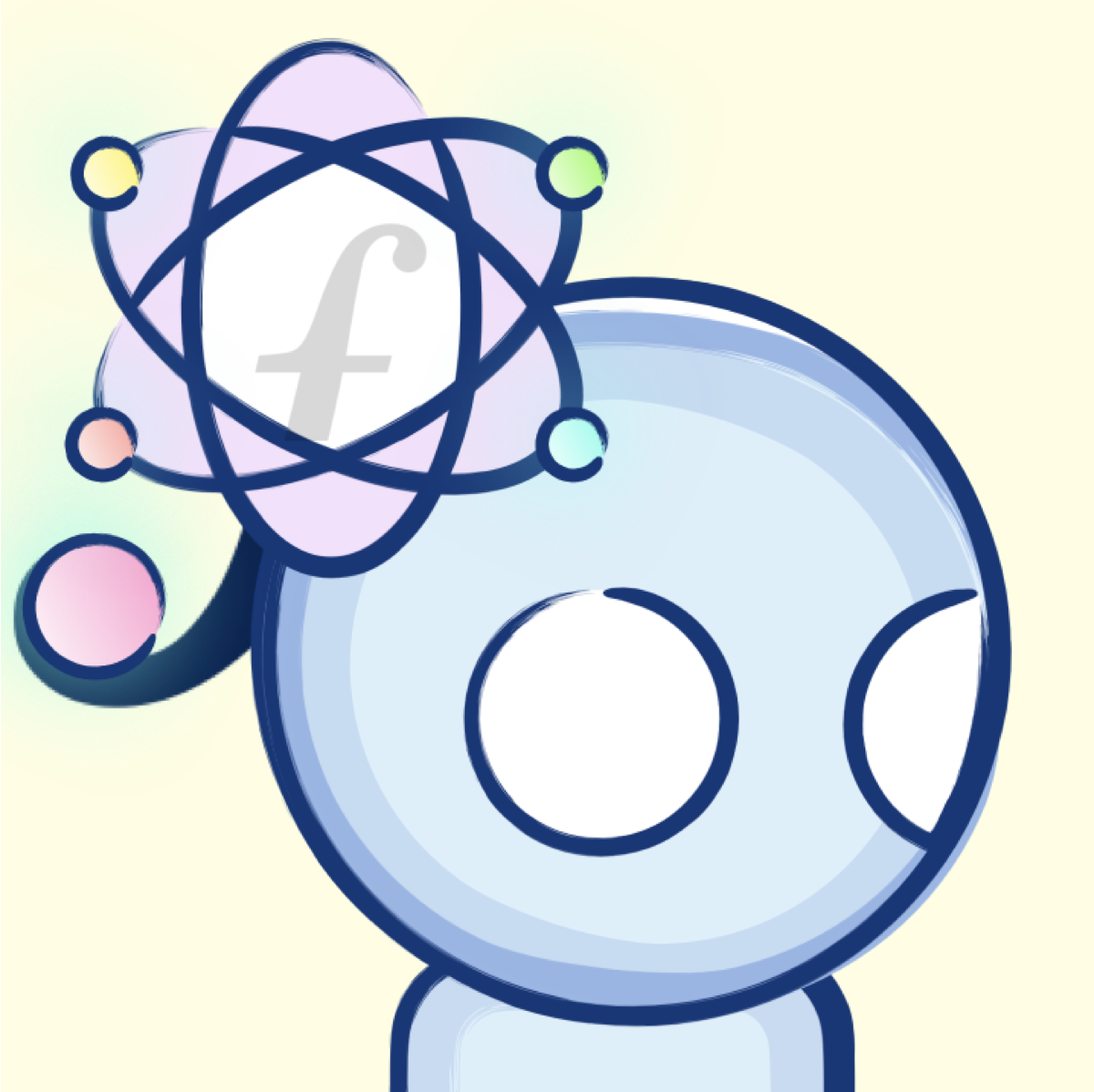
オイラーの定理では、Mとnが互いに素であることを前提にしています。
Mとnが互いに素でない場合の証明はより複雑になりますが、中国剰余定理を用いて同様の結果が導かれます。
6. 【補足】モジュラ逆数の求め方

秘密鍵はどうやって計算するの?
大きな数字だと毎回、しらみつぶしで探すのは大変だよね。
公開鍵 e と秘密鍵 d は、以下の関係になっていました。
これは、「φ(n)を法とする モジュラ逆数 の関係にある」といえます。
このモジュラ逆数は、ベズーの等式と関係があります。
ベズーの等式に a = e, b = φ を代入すると、互いに素なので gcd(e,φ)=1になります。
これを変形すると、

つまり、ベズーの等式での x を求めると 秘密鍵 d になるわけです。
6.1. ベズーの等式の整数解を求める
この x は、「ユークリッドの互除法」の考え方で計算できます。
たとえば、e = 13, φ = 20 の場合に、整数解 x, y を求めましょう。
通常は13x+20y=1の解は定まりませんが、整数解に限れば求まります。

ベズーの等式を満たす 13×(-3)+20×2 = 1 において、両辺で20で剰余を取ります。
13×(-3) ≡ 1 (mod 20)
d は 1< d < 20 なので、負数 -3 に 20 足した 17 が秘密鍵になります。


求めた y = 2 の方は、20の剰余を取る段階で打ち消されてしまいます。
6.2. 拡張ユークリッドのアルゴリズム
これをプログラムにすると、
def mod_inverse(e, phi):
a, b = e, phi
x0, x1 = 1, 0
while b != 0:
q = a // b
x0, x1 = x1, x0 - q * x1
a, b = b, a % b
if a != 1:
raise ValueError("モジュラ逆数が存在しません")
return x0 % phi基本的な考え方は、
- 商を使ってxを更新していきます。
- q = a ÷ b
- 新しい x0 = 古い x1
- 新しい x1 = 古い x0 – q * 古い x1
この更新式では、ユークリッド互除法の各ステップを「逆算」しているといえます。
- あとは、通常のユークリッド互除法と同様に、大きい数を小さい数で割った余りを求めて、割り切れるまで繰り返します。
- 新しい a = 古い b
- 新しい b = 古い a % 古い b
この計算ループを実行すると、
| ステップ | q | x0 | x1 | a | b |
|---|---|---|---|---|---|
| 初期値 | – | 1 | 0 | 13 | 20 |
| 1 | 0 | 0 | 1 | 20 | 13 |
| 2 | 1 | 1 | -1 | 13 | 7 |
| 3 | 1 | -1 | 2 | 7 | 6 |
| 4 | 1 | 2 | -3 | 6 | 1 |
| 5 | 6 | -3 | 20 | 1 | 0 |
def mod_inverse(e, phi):
x0, x1 = 1, 0
a, b = e, phi
print(f"| q | x0 | x1 | a | b |")
print(f"|---|----|----|---|---|")
print(f"| - | {x0} | {x1} | {a} | {b} |")
while b != 0:
q, a, b = a // b, b, a % b
x0, x1 = x1, x0 - q * x1
print(f"| {q} | {x0} | {x1} | {a} | {b} |")
if a != 1:
raise ValueError("モジュラ逆数が存在しません")
return x0 % phi
# 使用例
e = 13
phi = 20
try:
d = mod_inverse(e, phi)
print(f"公開指数: {e}")
print(f"φ(n): {phi}")
print(f"秘密指数: {d}")
print(f"検証: {(e * d) % phi == 1}")
except ValueError as error:
print(error)eのモジュラ逆数は 最後の x0 % φ です。
つまり、13 * x mod 20 ≡ 1 が成り立つ x は、
-3 % 20 = 17 で求められました。


(補足)
- φ(n) はオイラーのトーシェント関数
- 単純に (m**d) % n と計算すると、中間結果が膨大な大きさになり、大きな数値を扱う際、浮動小数点数の精度の問題が発生します。pow() 関数は、モジュラ指数演算のアルゴリズム(例:モンゴメリ乗算)を使用して、効率的に計算を行います。