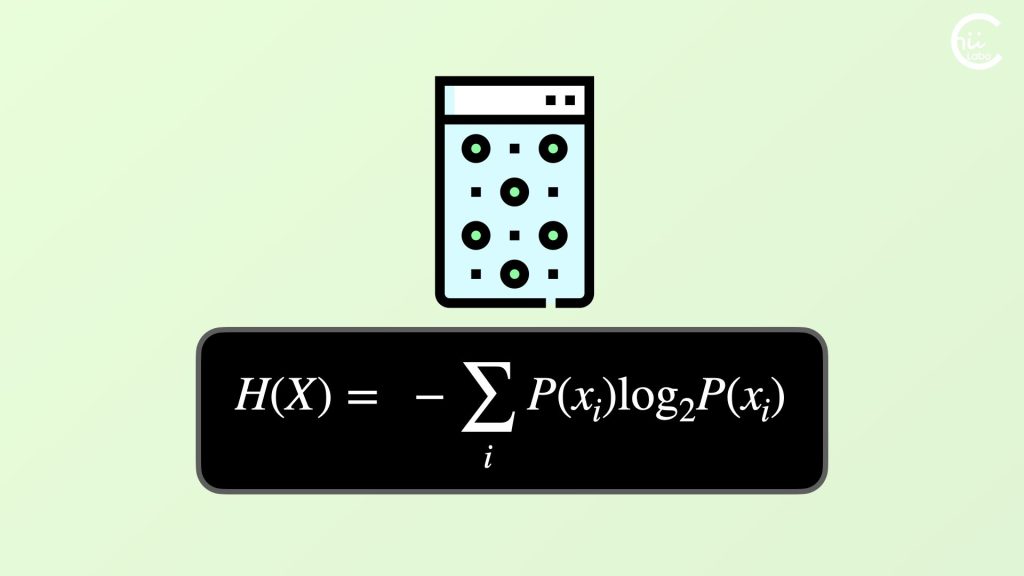- パスワードの「強さ」を示す指標として「エントロピー」が使われ、パスワードの取りうるパターン数の2を底とする対数で計算されます。
- パスワードに含まれる文字の種類を増やしたり、文字数を増やしたりするとエントロピーが高くなります。
- 一般に「英数記号12文字以上のパスワード」が推奨されるのは、エントロピーを高くするためです。

ただし、総当たり攻撃への耐性を高めるには、「完全にランダム」なパスワードにする必要はありません。
独自のルールなら、ある程度規則性があっても大丈夫です。
1. 情報理論におけるエントロピー

エントロピーって理科では聞いたことがあるけど、パスワードとなんの関係があるの?
情報理論における「エントロピー」は、
情報源から発生するメッセージの 予測不可能性 を定量化したものと言えます。

「エントロピー」は、熱力学と情報理論において、システムの乱雑さや無秩序さを表す尺度として使用される概念です。
離散確率変数 X がとる値を x1, x2, …, xn、
それぞれの確率を p(x1), p(x2), …, p(xn) としたとき、
Xのエントロピー H(X) は、以下の式で定義されます:
定義は複雑です。
しかし、「n個の事象が等確率で起こる」場合に限定にすると、
H(X) = -Σ p(xi) log2 p(xi)
= – n * (1/n) * (log2 (1/n)
= log2 n
つまり、組合せ数の 2を底とする対数を取ればよいわけです。

対数の底を2にすることで、情報理論における基本的な情報量の単位と整合性が取れるようになっているのです。
1ビットの情報量は、「2つの事象が等確率で起こる」ことを意味します。
このときのエントロピーを計算すると、
H(X) = -Σ p(xi) log2 p(xi)
= -(1/2 * log2(1/2) + 1/2 * log2(1/2))
= -(1/2 * (-1) + 1/2 * (-1))
= 1

つまり、1ビットの情報量は、エントロピーが1のときに得られる情報量に相当しています。
熱力学における物理エントロピーの定義は
dS = đQ / T
ここで、dSはエントロピーの微小変化、đQは系に加えられる熱量、Tは絶対温度を表します。

1.1. どうしてエントロピーは情報量の尺度に使えるの?
エントロピーは、情報量として解釈するのに都合の良い性質を持っています。
計算したエントロピーの性質は、この情報量に適しています。
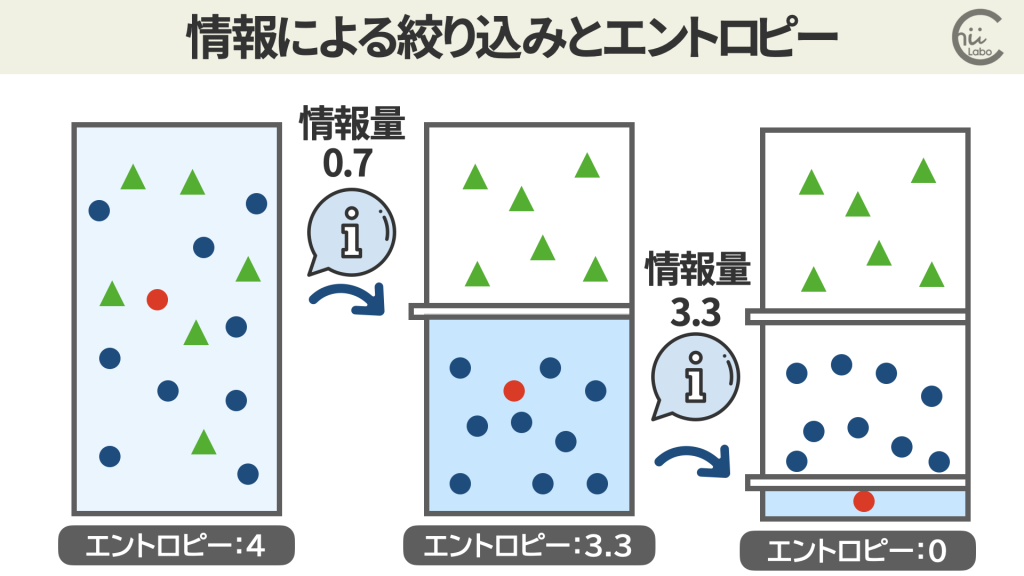
まず、珍しいことが分かった時ほど「得られた情報量は大きい」と言えるでしょう。
エントロピーの計算では、確率 p(xi) が小さいほど、-log2 p(xi) の値が大きくなります。
また、情報量とは「どれぐらい世の中の不確実性が減ったか」に対応します。
「情報を得ることで不確実性は減少」し、「複数の情報を組み合わせると、情報量は足し合わされる」と言えます。
エントロピーは、H(X,Y) = H(X) + H(Y|X)、複数の独立な確率変数の結合エントロピーについて加法性を満たします。
ルーレットの出目が分からない状態から、「出目は偶数である」という情報を得れば、不確実性は減ります。
さらに、「出目は1〜10の間」「出目は偶数」という2つの情報を合わせると、「出目は2,4,6,8,10のいずれか」に限定されます。
これも情報量が増えたとみなせます。

人間の直感とも矛盾せず、かつ数学的にも扱いやすい指標となっているのです。
2. パスワードの複雑さ・強さ
「エントロピー」は、パスワードの「強さ」を測る尺度としても使われます。
特に「手がかりなし」の総当たり攻撃に対する強さを表します。
パスワード攻撃のパターンはいくつかあります。

このような不正アクセスに備えるためには、ある程度パスワードを複雑にしておく必要があります。
「総当たり」で調べる範囲が広いほど、見つけ出すのに時間がかかることになります。
そこで、パスワードの取りうるパターン数をもとに、2を底に取った対数を計算します。
| パターン数 | エントロピー | |
|---|---|---|
| 数字4桁 | 10000 | 13.3 |
| 英数8文字 | 2.18 * 1014 | 47.6 |
| 英数記号12文字 | 5.40 * 1023 | 78.8 |
| 誕生日 | 366 | 8.5 |
| 英単語そのまま | 約50000 | 15.6 |
つまり、パスワードの検索範囲のエントロピーが
1増えると、かかる時間は2倍に、
10増えると 1024倍になります。

「パスワードのエントロピー」というのは、パスワードそのものの特徴というよりは、パスワードが含まれる検索範囲の広さを表しています。
2.1. パスワードのエントロピーを計算する
たとえば、数字・英字をランダムに8文字組み合わせるパスワードのエントロピーを計算してみます。
1文字ごとの可能性は26(英字の小文字)+ 26(英字の大文字)+ 10(数字)= 62通りです。
つまり、1文字当たりのエントロピーは log2(62) = 6.0ビット。
8文字だと エントロピーは 47.6ビットになります。

エントロピーは対数なので、そのまま文字数で掛け算にできます。
これが数字を4文字組み合わせるパスワードの場合は、
log2(10000) = 13.3ビット。
一方、記号・数字・英字をランダムに組み合わせるパスワードの場合についても考えます。
有効な記号の種類にもよりますが、一例として各文字の可能性を 26(英字の小文字)+ 26(英字の大文字)+ 10(数字)+ 33(記号)= 95通りとすると、
1文字当たり log2(95) =6.57ビット。
つまり、記号・数字・英字のランダム12文字のパスワードのエントロピーは 78.8ビットになります。


記号などの文字種を増やさなくても、文字数を増やすことでもエントロピーは増えるんだね。
3. パスワードの手がかりを与えない
また、「手がかりなし」というのもポイントになります。
誕生日や単語など「意味のある文字列だけ」で構成すると、エントロピーは大きく減り、総当たりでも探しやすくなってしまいます1。
このようなよく使われるパスワードは、まず辞書攻撃の対象になるからです。
一方、数字だけのパスワードであれば明らかに弱いです。
しかし、それは「ハッカーがあなたが数字だけのパスワードを使っていることを知っている」という場合に限られます。
そのような手がかりがなければ、ハッカーは可能な文字の完全なリストを使って総当たり攻撃をしなければならないので、やっぱり時間がかかります。

「手がかり」によってエントロピーを低くなってしまうんだね。
3.1. パスワードに文字を詰める(Password Padding)
また、パスワードの強度は、単純にエントロピーだけでも決まりません。
以下の例では、上のパターンの方が規則的で、数学的な意味でのエントロピーは低いです。

しかし、「総当たり攻撃」への耐性として考えると、実際には同等の強度を持つと考えられます。
一般に攻撃者には、情報を選んできた基準(手がかり)が伝わらないからです。
ENTROPY: If you are mathematically inclined, or if you have some security knowledge and training, you may be familiar with the idea of the “entropy” or the randomness and unpredictability of data. If so, you’ll have noticed that the first, stronger password has much less entropy than the second (weaker) password. Virtually everyone has always believed or been told that passwords derived their strength from having “high entropy”. But as we see now, when the only available attack is guessing, that long-standing common wisdom . . . is . . . not . . . correct!
GRC | パスワードの山: あなたの針はどれだけ隠されていますか?
記号をパスワードに詰めると文字数を増やすことができます。
ただし、「.」は単純過ぎるかもしれません。
独自のパターンを決める方がよいです。

「パスワードの複雑さ」は、パスワード攻撃への強さの要素の一つですが、必ずしもそれだけで決まるわけではないのですね。
4. 解析時間は何とも言えない

パスワードはエントロピーがいくつ以上ならいいの?
実は、理論的にいくつ以上であれば「安全」と言えるわけではないのです。
というのも、パスワードを調べ上げるのにかかる時間は、一概には言えません。
よく知られたパスワードの解析時間に関する表を見ると、同じパスワードの複雑さでも記載されている時間が異なります23。

1パターンを調べるのにどれぐらいの処理時間がかかるかは、システム次第だからです。
つまり、「ある仮定のもとで想定される処理時間」ということになります。
たとえば、GRCの例では、1秒間に調べるパターンを、1000、1000億、100兆の3つのケースを想定して、かかる時間を計測しています。
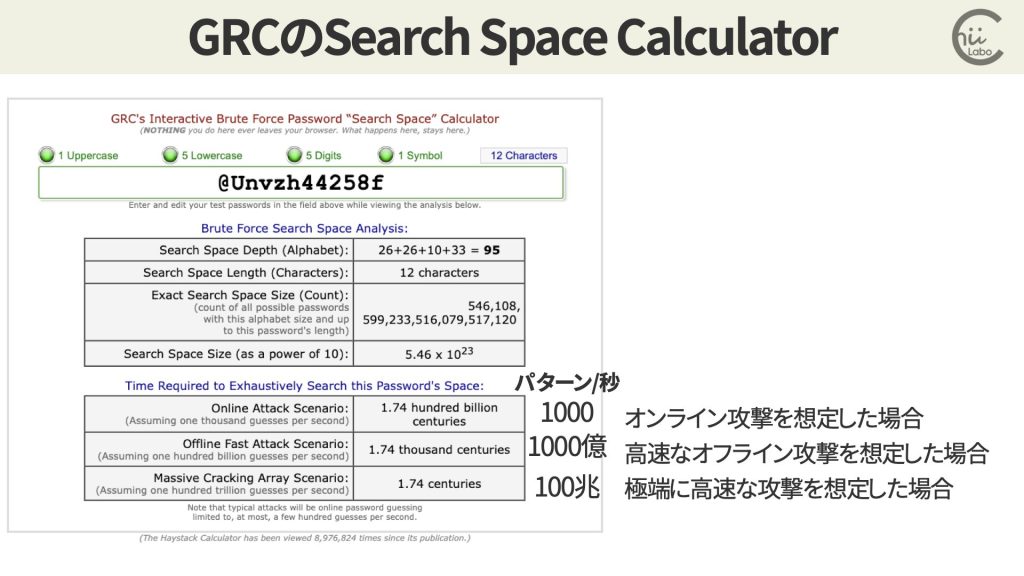
ただし、一般的な設計のウェブサイトであれば、パスワード入力フォームに総当たり攻撃を高速に実行することは困難です。
セキュリティ対策によって、数回のログイン試行に失敗すると一定時間アクセスが制限されるからです。

大ざっぱに言えば、「めちゃくちゃ速いケースでも、めちゃくちゃ時間がかかるはずだから大丈夫だろう」というだけの話なのです。
4.1. 75ビットのエントロピーが一般的
個人のパスワードの場合、一般には 75ビット以上のエントロピーであることが推奨されます4。
この複雑さであれば、現在の技術では総当たり攻撃での解読が困難だと考えられています。
「英数記号12文字以上のパスワードを作りなさい」というのは、これが根拠です。

どうせ記憶させるなら、うんと複雑なパスワードにすればいいのに。

建物の「耐震基準」みたいな感じで、専門家が共通に考える水準をクリアすれば「安全」とみなしてよいんだろうね。
4.2. より厳しい基準でも128ビット
最近の計算機は、分散処理の工夫などでパスワードの計算時間が短縮しています。
そのため、現在のセキュリティの専門家は、さらに厳しい 128ビット以上のエントロピーを持つことを推奨するようになってきています。
これは、英字、数字、記号だと20文字以上(英数字だけだと22文字〜)ランダムにつなげたパスワードに相当します。

一般的なサービスで要求されるルールより、かなり複雑です。
このレベルなら、暗号化したパスワードのデータベースに侵入された場合でも解読は事実上不可能になります。

しかし、それでもいずれは計算能力の進歩で実時間の中で解読可能になるかもしれません。

いろいろ理屈は難しいけど、結論はわりと普通のことだね。



(補足)
- たとえば、英単語は5万語として計算しています- 大人語を捨てると、英語は途切れない!? [英語] All About
- How Secure is Your Password? – gHacks Tech News
- パスワード解析されるまでの時間をまとめてみた【パスワードクラッキングについて】
- パスワードには、少なくとも75ビットのエントロピーがあることが推奨されています。 – パスワードエントロピーとは何か?それが重要な理由