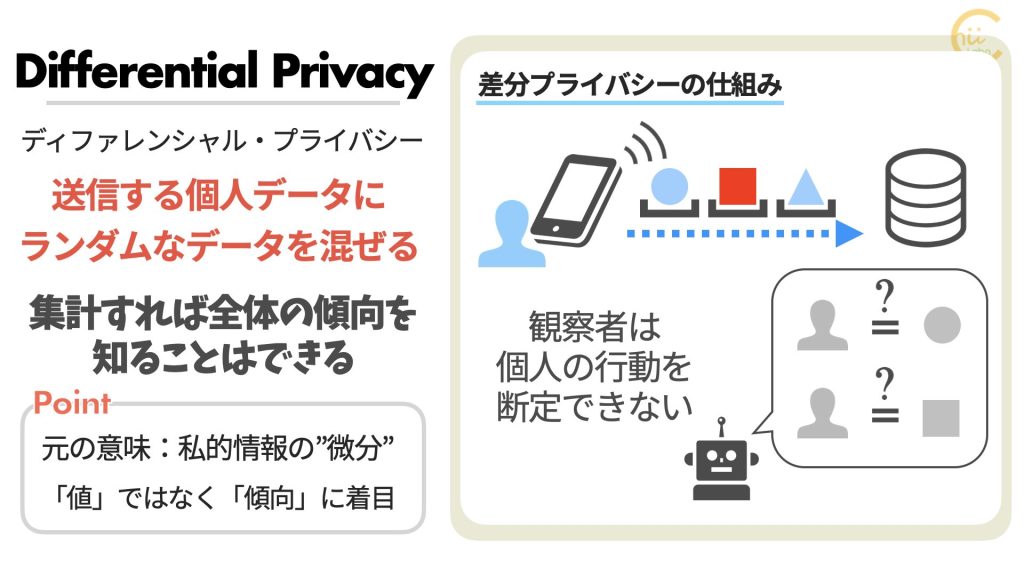
ベイジアンフィルタとは？（ベイズの定理とスパム判定）

「ベイジアンフィルタ」は、条件付き確率の考え方（ベイズの定理）をもとに迷惑メールである確率を計算する、古典的な手法です。
過去のスパムメールと非スパムメールから単語の出現頻度の違いを学習して、新しく受信メール内の単語の組み合わせからスパム確率を計算するのが特徴です。
ただし、判断材料が単語の出現頻度に依存しているため、正しいメールに似せた文章だとスパムと見分けられないことがあります。

たとえば、「高額なプレゼントに当選しました！」などのような、独特のスパムメールには有効です。

ベイジアンフィルタの基本的なアルゴリズム

トークン化
トークンの出現頻度の学習
スパム確率の計算
メール全体のスパム確率の計算
スパム判定
自動学習

1. ベイジアンフィルタとベイズの定理

「ベイズの定理」は、事前確率と条件付き確率（尤度：likelihood）から事後確率を計算するための定理です。

ベイズの定理

P (A | B) = P (B | A) * P (A) / P (B)

P(A): 事象Aが起きる確率（事前確率）
P(B): 事象Bが起きる確率（事前確率）
P(B|A): 事象Aならば事象Bが起きる条件付き確率
P(A|B): 事象Bならば事象Aが起きる条件付き確率

「事象Bが起きているなら、事象Aの確率は〜だ」ということができます。

ベイズの定理は、新しい情報が得られた際に、事後確率を更新するために使えます。

確率論の基本的な定理の一つであり、ベイズ統計学の基礎となっています。

目次に戻る

1-1. ベイジアンフィルタでの応用

ベイジアンフィルタは、「ベイズの定理」をスパム判定に応用しています。
スパム判定での「新しい情報」とは、「スパムに多そうな単語が出現していること」です。

これがわかれば、「このメールはスパムの可能性が濃厚である」と言えるからです。

例えば、

「お金」という単語がスパムメールに多く含まれているとします。
新しいメールに「お金」という単語が含まれていた場合、そのメールがスパムである「条件付き確率」が高くなります。

つまり、スパム判定では、

事象Aは「スパムメールである」
事象Bは「『お金』という単語が含まれる」

に相当します。

事前確率（P(A)、P(B)）と条件付き確率（P(B|A)）をもとに事後確率（P(A|B)）を計算し、一定の閾値を超えればそのメールを「スパムであろう」と判断します。

事前確率の設定:
「メールがスパムである確率」と「スパムでない確率」の事前確率（prior probability）を設定します。
尤度（条件付き確率）の計算:
学習データから、メールに含まれる単語がスパムメールとスパムでないメールのどちらに多く出現するかの尤度（likelihood）を計算します。
事後確率の計算:
ベイズの定理を用いて、事前確率と尤度から「メールがスパムである」事後確率（posterior probability）を計算します。
判断:
事後確率が一定の閾値を超えた場合、そのメールをスパムと判断します。

目次に戻る

2. トークン化と出現頻度の学習

ベイジアンフィルタは、まずメールの本文をトークン（単語や記号）に分割します。
この過程では、ストップワード（”the” や “and” など）が除去され、ステミング（単語を語幹に変換すること）が行われます。

次に、ベイジアンフィルタは、事前に分類されたスパムメールと非スパムメール（ハムメール）のデータセットを使用して、各トークンの出現頻度を学習します。
この学習データは、ユーザーが提供したメールや、自動学習機能によって収集されたメールから取得されます。

これが「事前確率」になります。

目次に戻る

2-1. 受信メール内のトークンごとのスパム確率を計算する

新しいメールを受信すると、ベイジアンフィルタはそのメールに含まれるトークンを抽出し、各トークンのスパム確率を計算します。

「トークンのスパム確率」は、そのトークンがスパムメールに出現する頻度と、ハムメールに出現する頻度から計算されます。

例えば、

“無料”や”当選”といった単語は、スパムメールで高い頻度で使われる傾向があります。

このようなスパムメールに頻繁に出現し、ハムメールにはほとんど出現しないトークンのスパム確率を高く計算します。

ベイジアンフィルタでは、ある単語 Wを含むメールがスパム(S)である確率 P(S|W)を計算します。

P (S | W) = \frac{P (W | S) P (S)}{P (W | S) P (S) + P (W | H) P (H)}

P(S|W): 単語Wを含むメールがスパムである条件付き確率
P(W|S): 単語Wがスパムメールに含まれる条件付き確率
P(S): メールがスパムである確率
P(W|H): 単語Wがハムメール(非スパム)に含まれる条件付き確率
P(H): メールがハムである確率

分母がやや複雑になっているのは、単語 W を含まないメールもあるからです。

目次に戻る

2-2. メール全体のスパム確率によって判定する

各トークンのスパム確率を計算できると、全ての単語についての確率の積を取ることで、メール全体のスパム確率を計算します。

計算されたメール全体のスパム確率が、設定された閾値（bayes_threshold）を超えた場合(例えば0.5以上であれば)、「そのメールはスパムである」と判定されます。

目次に戻る

2-3. 機械学習によって調整していく

「ベイジアンフィルタ」は、ナイーブベイズ分類器（Naive Bayes Classifier）と呼ばれる機械学習アルゴリズムに基づいていて、教師あり学習をします。

自動学習機能が有効な場合、受信したメールは「スパム」または「ハム」として学習データに追加されます。
ユーザーがメールを手動で分類すると、フィルタがその判断を自動的に学習していきます。
また、ユーザーごとに学習データを保持できるため、個々のユーザーに合わせたスパム判定が可能です。

目次に戻る

3. ベイジアンフィルタは文脈を無視する

ベイジアンフィルタは比較的古典的な迷惑メールフィルタリングのアルゴリズムと言えます。

1990年代後半から2000年代初頭にかけて広く使用され、当時は、スパムメールの判定に機械学習の手法を取り入れた革新的で有効な手法でした。

しかし、ベイジアンフィルタには弱点があります。

ベイジアンフィルタは各単語の出現頻度のみに着目し、基本的には文脈が無視されることです。
そのため、文脈によって意味が変化するような単語を含むメールを、正しく判定できない場合があります。

また、この性質をスパマーが悪用すると、意図的に”正しいメールっぽい”単語を含めるようになります。
そうすると迷惑メールを「正しい」と誤判定してしまいがちです。

現在では、

ベイジアンフィルタに加えて、サポートベクターマシン（SVM）、ニューラルネットワーク、トランスフォーマーなどの手法が組み合わせて使用されることが多くなっています。

これらの手法では、単語の出現位置や順序も考慮した複雑な判定ができるため、ベイジアンフィルタとは異なるアプローチでスパムメールを検出することが可能です。

正規分布のグラフの図示（p5.js）

function setup() {
  createCanvas(600, 400);
}

function draw() {
  background(255);
  
  // パラメータ
  let mu = 0;  // 平均
  let sigma = 1;  // 標準偏差
  
  // x軸の描画
  drawXAxis();
  
  // 正規分布の描画
  drawNormalDistribution(mu, sigma);
}

// x軸の描画
function drawXAxis() {
  stroke(0);
  line(0, height/2, width, height/2);  // x軸
}

// 正規分布の描画
function drawNormalDistribution(mu, sigma) {
  noStroke();
  fill(0, 0, 255, 100);
  
  beginShape();
  vertex(0, height/2);
  for (let x = -3; x <= 3; x += 0.1) {
    let y = normalDistribution(x, mu, sigma);
    let px = map(x, -3, 3, 0, width);
    let py = map(y, 0, 0.4, height/2, 0);
    vertex(px, py);
  }
  vertex(width, height/2);
  endShape(CLOSE);
}

// 正規分布の確率密度関数
function normalDistribution(x, mu, sigma) {
  return (1 / (sigma * sqrt(TWO_PI))) * exp(-((x - mu) ** 2) / (2 * sigma ** 2));
}

こちらもどうぞ。